11 KiB
5. ПРЕДСТАВЛЕНИЕ СОЦИАЛЬНОЙ СЕТИ ГРАФОМ БОЛЬШОЙ РАЗМЕРНОСТИ, АНАЛИЗ СВЯЗЕЙ
Как уже было отмечено выше социальные сети, их сегменты, а также связи в них принято представлять в виде графа. Рассмотрим основные понятия теории, необходимые для введения в анализ социальной сети, представленной графом.
Граф – это упорядоченная пара `G = (V, E)`, где `V (vertices)` – множество вершин (узлов) графа, а `E (edges)` – множество ребер. Граф может быть как ориентированным, так и неориентированным (рис. 17).
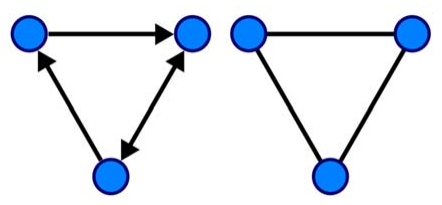
Рис. 17. Ориентированный и неориентированный графы
C точки зрения социальных сетей ребра в неориентированном графе могут описывать такую связь как «дружба», а в ориентированном – «подписку». Граф, представляющий социальную сеть, также может быть и смешанным – имеющим как ориентированные ребра, так и неориентированные.
Граф `G = (V, E)` , с `|V| = n` вершинами может быть представлен в виде симметричной бинарной матрицы размерности `n \times n`:
A(i,j) = \begin{cases}
1, &\text{если $v_i$ связана ребром с $v_j$},\\
0, &\text{в иных случаях}.
\end{cases}
Если граф ориентированный матрица `A` не будет симметричной.
Если граф взвешенный (ребру которого поставлено в соответствие некое число – вес) матрица `A` имеет вид
A(i,j) = \begin{cases}
w_{ij}, &\text{если $v_i$ связана ребром с $v_j$},\\
0, &\text{в иных случаях}.
\end{cases}
где `w_{ij}` – вес ребра, соединяющего вершины `v_i` и `v_j`.
Опираясь на матричное представление графа множество наборов данных, социальных сетей и не только можно представить в виде графа.
Пусть `D = \{x_i\}_{i=1}^n` – исходный набор данных. Определим взвешенный граф `G = (V, E)` с весом ребер
w_{ij} = sim(x_i, x_j),
где `sim(x_i, x_j)`, описывает зависимость между `x_i` и `x_j`.
Таким образом, исходный набор данных `D = \{x_i\}_{i=1}^n` будет представлен взвешенным графом. В случае с социальной сетью, отыскание зависимостей является тривиальной задачей.
Граф `H = (V_H, E_H)` называется подграфом графа `G = (V, E)`, если `V_H \subseteq V` и `E_H \subseteq E`. Такой граф может использоваться для выделения сообщества в социальной сети.
Наиболее распространёнными задачами в рамках анализа социальных сетей, решаемых с помощью теории графов, являются:
- Подсчёт пользователей и связей при помощи определения количества вершин и рёбер.
- Поиск зависимостей и связей через нахождение компонент связности в графе.
- Наличие сообществ в социальной сети, как правило, при помощи кластерного анализа графа.
- Принадлежность профиля (вершины графа) к тому или иному сообществу (кластеру или подграфу).
- Роль и влияние конкретных пользователей друг на друга и на сообщества (роль и значимость каждой вершины в графе).
- Моделирование социальных сетей, в том числе посредством определения средней плотности графа.
Вершины и рёбра графа называются также элементами графа, число вершин в графе `|V|` – порядком, число рёбер `|E|` – размером графа.
Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром.
Цепью принято называть маршрут, ребра которого различны. В ориентированном графе цепь является путём. Длина цепи – это количество входящих в неё рёбер.
Циклом называют цепь, первая и последняя вершины которой совпадают. Длиной пути (цикла) называют число составляющих его рёбер.
Граф называется связным, если любые две его вершины связаны маршрутом.
Компонента связности графа `G = (V, E)` – его подграф `H = (V_h, E_H)`, образованный на подмножестве всех вершин `V_H`, которые можно соединить произвольным маршрутом.
Связный граф состоит из единственной компоненты связности. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины. Ребро графа называется мостом, если его удаление увеличивает число компонент.
Расстояние между вершинами графа – длина кратчайшей цепи, соединяющей эти вершины.
Эксцентриситет вершины графа − это максимальное расстояние от неё до других вершин (по количеству ребер или их весу).
Диаметром графа `d(G)` является максимальное расстояние между всеми парами вершин в графе `x_i` и `x_j`: `d(G) = maxd(x_i, x_j)`. Таким образом, диаметр графа − это максимальный из эксцентриситетов вершин.
Радиусом графа называется минимальный эксцентриситет среди всех вершин графа.
Центральной вершиной графа является вершина, чей эксцентриситет равен радиусу графа.
Периферийной вершиной графа является вершина, чей эксцентриситет равен диаметру графа.
При выделении сообщества принято сравнивать среднюю плотность связей внутри кластера и между кластерами, т.е. сообщество – это та часть графа, в которой средняя плотность между узлами превышает плотность связей между сообществами. Другими словами, внутри сообщества связей должно быть больше, чем между сообществами. Алгоритмы, описывающие выделение сообществ приводятся в соответствующем разделе данного учебного пособия.
Степенью вершины графа называется количество инцидентных ей рёбер. Последовательностью степеней вершин неориентированного графа является список степеней вершин, отсортированный по убыванию.
Пусть `N_k` – количество вершин графа со степенью `k`. Распределение частот степеней графа при этом `(N_0, N_1, \ldots, N_t)` , где `t` – максимальная степень вершины в графе.
Пусть `X` – случайная величина, обозначающая степень вершины. Распределение степеней в графе – есть функция вероятности `f` случайной величины `X`, обозначенная как
(f(0), f(1), \ldots, f(t)),
где `f(k) = P(X = k) = \dfrac{N_k}{n}` – вероятность вершины графа со
степенью `k`.
В качестве примера рассмотрим граф, изображенный на рис.18. Последовательность степеней вершин этого графа: `(4, 4, 4, 3, 2, 2, 2, 1)`.
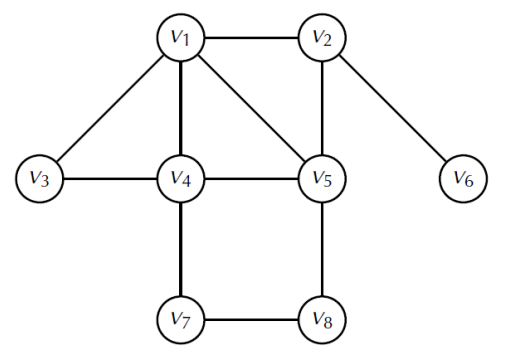
Рис. 18. Граф с восемью вершинами
Распределение частот степеней графа
(N_0, N_1, N_2, N_3, N_4) = (0, 1, 3, 1, 3).
Распределение степеней в графе при этом
(f(0), f(1), f(2), f(3), f(4) ) = (0, 0.125, 0.375, 0.125, 0.375).
Распределение степеней в графе может использоваться в моделировании социальной сети, представленной данным графом.